© 2023 yanghn. All rights reserved. Powered by Obsidian
6.3 填充和步幅
要点
- 填充和步幅是卷积层的超参数,是网络架构的一部分,不像学习率一样需要经常调整
- 填充在周围添加额外的行/列,来控制输出形状的减少量,步幅为 1 的情况下,记忆公式:$$输出图像大小 = 填充后的输入图像大小 - (核大小-1)$$ 通常取
,保持矩阵大小不变,方便计算(3x3 填充 1,5x5 填充 2,7x7 填充 3) - 步幅是每次滑动核窗口时的行/列的步长,可以成倍的减少输出,通常觉得计算量太大了,通常取 2
1. 填充
每次使用卷积层,都会使得矩阵的维度降低(每次形状大小减少
整个深度学习都是关于"深度"的,就是说通常训练很多层的网络,深度网络通常更擅长进行层次化的特征表示,能够用相对较少的参数更准确地近似复杂函数
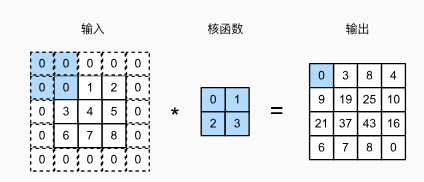
- 填充
行和 列, 输出形状为
- 通常取
,保持矩阵大小不变 - 当
为奇数:在上下两侧填充 - 当
为偶数:在上侧填充 , 在下侧填充
卷积核的高度和宽度通常为奇数,例如1、3、5或7。上下填充
import torch
from torch import nn
# 为了方便起见,我们定义了一个计算卷积层的函数。
# 此函数初始化卷积层权重,并对输入和输出提高和缩减相应的维数
def comp_conv2d(conv2d, X):
# 这里的(1,1)表示批量大小和通道数都是1
X = X.reshape((1, 1) + X.shape)
Y = conv2d(X)
# 省略前两个维度:批量大小和通道
return Y.reshape(Y.shape[2:])
# 请注意,这里每边都填充了1行或1列,因此总共添加了2行或2列
conv2d = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1))
X = torch.rand(size=(8, 8))
comp_conv2d(conv2d, X).shape #torch.Size([8, 8])
- 填充
行,保持大小不变。第 8 行: X.shape是一个元组,这里是把元组拼接起来 - 这里的
padding表示上下填充
2. 步幅
- 填充减小的输出大小与层数线性相关
- 给定输入大小
, 在使用 卷积核的情况下, 需要 44 层将输出降低到 - 需要大量计算才能得到较小输出
- 给定输入大小
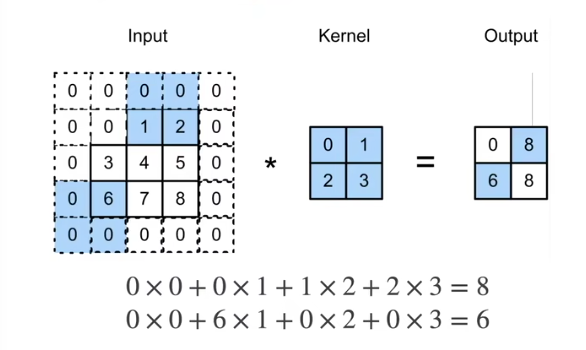
- 给定高度
和宽度 的步幅, 输出形状是( 、 表示输入图片的高宽, 、 表示核的高宽)
- 如果
- 如果输入高度和宽度可以被步幅整除
一般来说步幅取 2,如果长和宽都是偶数的话
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)
comp_conv2d(conv2d, X).shape # padding=1 输出形状不变,X.shape为偶数,直接除以stride
torch.Size([4, 4])